parallel algorithm course 04

---

synchronization has costs

---

simple list traversal

// linked list

p = head;
while (p) {
    process(p);
    p = p->next;
}

compute all p in advance

#pragma omp parallel for schedule(static, 1)
    for (int i = 0; i < count; ++i)
        process(parr[i]);

---

task

#pragma omp parallel {
    // not often used
    #pragma omp task
    foo();

    #pragma omp barrier

    // more common case
    #pragma omp single {
        #pragma omp task
        bar();
    }
}

example (with bug)

int fib(int n) {
    int x, y; // private
    if (n < 2) return n;

    #pragma omp task 
    // need `shared(x)`. by default, task copy the whole stack, 
    // x is in different address
    x = fib(n-1);

    #pragma omp task // need `shared(y)`, default is private in task
    y = fib(n-2);

    #pragma omp taskwait

    return x+y; // wrong here!!!
}

#pragma omp parallel single
fib(n);

two important points

1. barrier

2. data env

example 2 (with bug)

list ml;
Element *e;
#pragma omp parallel
#pragma omp single
{
    for (e=ml->first; e; e=e->next)
    #pragma omp task // need firstprivate(e)
        process(e); // has data racing
}

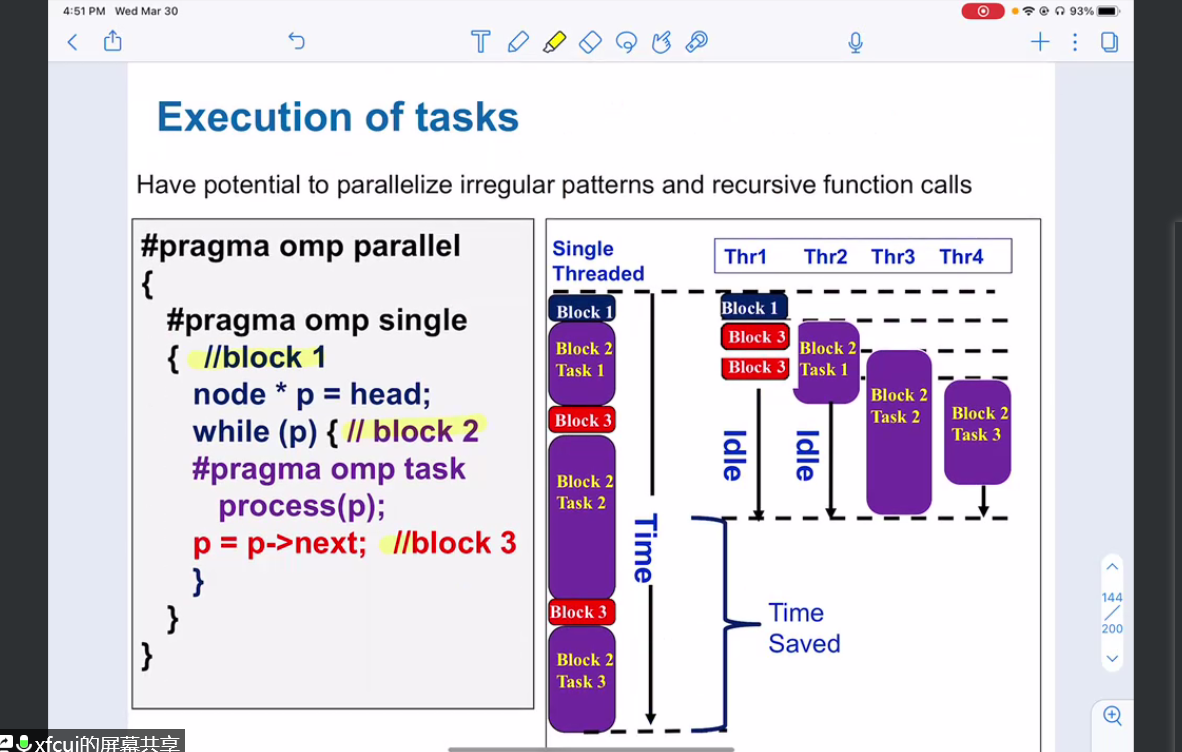
return to first example

#pragma omp parallel
{
    #pragma omp single
    {
        node* p = head;
        while(p) {
            #pragma omp task firstprivate(p)
                process(p);
            p = p->next;
        }
    }
}

running schema

---

merge sort

directly using parallel

\(T_1=2T_1(\frac{n}{2})+O(n)=O(n\cdot log(n)\)

\(T_\infty=T_\infty(\frac{n}{2})+O(n)=O(n)\)

---

use a differernt merge method

parallel merge

say here we have two sorted seqs (\(\le\))

\(A=a_1,\dots,a_n\) and \(B=b_1,\dots,b_n\)

let \(t=a_{\lceil \frac{n}{2}\rceil}\), split A and B into sub arr \(A_1,A_2,B_1,B_2\) s.t. \(A_1\le t, B_1\le t\) and \(A_2\gt t, B_2\gt t\)

so seq \(A_1,B_1,A_2,B_2\) is semi-merged by t, then go on with \(merge(A_1,B_1)\) and \(merge(A_2,B_2)\)

random number generating problem

problem

example: approximate \(\pi\) using Monto Carlo

seed(SEED);
#pragma omp parallel for private(x,y) reduction (+:n_in_circle)
for(int i = 0; i < num_trials; i++) {
    x = random();
    y = random();

    if (x*x + y*y <= r*r) n_in_circle ++;
}

pi = 4.0 * (1.0 * n_in_circle / num_trials);

---

Linear Congruential Generator(LCG) (has data racing problem)

int random_last = 0;
// need 
// #pragma omp threadprivate(random_last)

int random() {
    random_next = (MULTIPLIER * random_last + ADDEND) % PMOD;
    random_last = random_next;

    return random_next;
}

parameter: (one possible parameter suite) MULTIPLIER=1366, ADDEND=150889, PMOD=714025

has a period (less than PMOD)

---

single thread and multi-thread has different accuracy (multi-thread has poor performance)

data racing on var random_last

solution 1

add #pragma omp threadprivate(random_last) under int random_last=0

has a local copy of random_last when creating a thread

similar to firstprivate

problem: still poor than single thread version

different random range in threads maybe overlap

solution 2

Leap Frog method

generate different seeds for each thread

situation for ADDEND=0

#pragma omp single
{
    nthreads = ...
    iseed = PMOD / MULTIPLIER;
    pseed[0] = iseed;
    mult_n = MULTIPLIER;
    for (int i = 0; i < nthreads; i++) {
        iseed = (unsigned long long) ((MULTIPLIER * iseed) % PMOD);
        pseed[i] = iseed;
        mult_n = (mult_n * MULTIPLIER) % PMOD;
    }
    id = ...
    random_last = (unsigned long long) pseed[id];
}