parallel algorithm course 09

parallel alg

• array

• linked list

• tree (to list)

• graph (today)

parallel BFS

BFS(G[V,E],S)

D[V] = inf
D[S] = 0

F = {s}

while F not empty do {
    v = pop(F)
    for (v, w) in E do {
        if D[w] = inf {
            D[w] = D[v] + 1
            push(F, w)
        }
    }
}

key idea: layering \(F_l\)

need a data structure:

• allow repetitive occurance of elements

• unordered

• fast search union and split

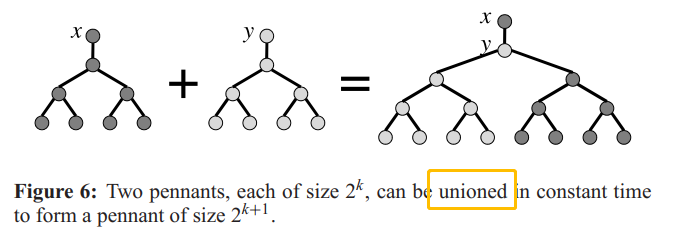
Bag of pennats

• A pennant: \(2^k\) nodes

• add an extra root to a balance binary tree

• union, split

• a bag of pennants can be mapped to a binary number

• insert -> add one (\(O(\log n)\))

• combine two bags of pennants -> binary number adding (\(O(\log n)\))

• split -> require balance (\(O(\log n)\))

bag of pennant

// calculate F(l+1) given F(l)
initialize(F(l+1), an empty pennant)

fun process-level (G, F(l), F(l+1), D)
if |F(l)| > threshold {
    Fa, Fb = split(F(l))
    spam {
        process-level (G, Fa, F(l+1), D)
        process-level (G, Fb, F(l+1), D)
    }   
    sync
} else {
    foreach v in F(l)
    par-for (v, w) in E do {
        if D[w] = inf {
            D[w] = D[v] + 1
            insert(F(l+1), w)
        }
    }
}

extend

matrix A, B, C

\(A\times B=C\)

tile

consider \(A^k\)

save \(A\), \(A^T\)